02/07
_ [プログラミング] 5×5のマス目に6個の○を次の条件を満たすように全部書く を3通りで解いてみる
小飼弾氏の1/24のエントリ「Math - 5×5のマス目に6個の○を次の条件を満たすように全部書く」が面白そうで、2週間遅れながら解いてみました。
問題に挑戦してみたい方は、途中までで読むのを止めてみてください。
問題
5×5のマス目に6個の○を次の条件を満たすように書きます。
条件:各行・各列に少なくとも1個は○を書く。同じマスには2個以上の○を書くことはできない。
このとき、6個の○を書く方法は全部で何通りありますか。
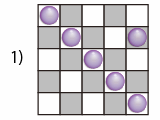
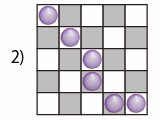
解答1: 力押し
プログラミングで力押しで解いてみます。
- 1つずつ6カ所に置いてみる
- 同じ配置は調べ直さないように、左上(0)から右下(24)方向にだけ辿る
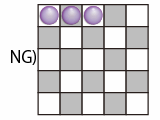
- 残りをどう配置しても条件を満たせないときにはそこで探索を打ちきる (NG図)
そうしてごり押し気味に書いてみたRubyのソースコード。変数や関数の名前は適当です。
def f(a, d, s) r = 0 s.upto(24) do |i| a[d] = i x = {} y = {} 0.upto(d) do |j| x[a[j] / 5] = true y[a[j] % 5] = true end if (x.size >= d) && (y.size >= d) if (d == 5) r += 1 else r += f(a, d+1, i+1) end end end r end a = [0]*6 puts f(a, 0, 0)
解答2: 途中経過を詳しく見る
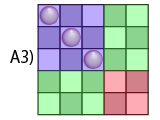
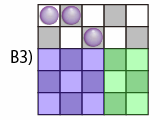
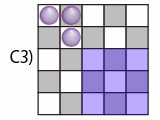
手で解けるようにもう少し分類します。6個置いたときに条件を満たせるように途中k個置く方法は、次の3通りがあります。
- A: k個で縦横ともにk列通っている。次の1個を置くと、その場所によってA(赤), B(緑), C(青)に進む。
- B: k個で縦横の一方はk列、もう一方は(k-1)列通っている。次の1個を置くと、その場所によってB(緑), C(青)に進む。
- C: k個で縦横ともに(k-1)列通っている。次の1個を置くと、その場所によってC(青)に進む。
図は○を3個置いたときのもの。この方法なら、先ほどよりは高速に解けそうです。
a = 25 b = c = 0 1.upto(5) do |i| a, b, c = (5-i)**2*a, 2*i*(5-i)*a+(5-i)*(6-i)*b, (i*i-i)*a+(6-i)*i*b+(6-i)**2*c end puts c/(6*5*4*3*2)
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| A | 25 | 400 | 3600 | 14400 | 14400 | 0 |
| B | 0 | 200 | 7200 | 86400 | 288000 | 0 |
| C | 0 | 0 | 2400 | 108000 | 1296000 | 3024000 |
今度は同じ場所を何度も通るため、最後に6!で割り算。これで終了です。
私の最初の解答はこの方法でした。紙に状態図を描いて。「3×4のマス目の左上から右下に最短距離で進む方法は何通りですか?」で、各交差点の場合を全て書き出す感じです。
解答3: 最終結果を詳しく見る
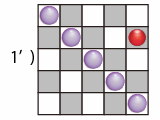
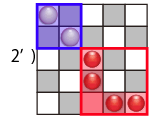
…一応それでも解けますが、7桁の数は手書きするには厳しいでしょうと(汗)。もっと簡単に解けるはずと、途中経過は無視して最終結果だけ眺めてみました。
最初の図をよく見ると、この条件を満たす方法は2通りしか無いことが分かります。
- 1: 5つの○で全ての縦横を埋め尽くし、最後1つはどこに置いても良い
- 2: 5つの○で全てを埋め尽くす事はできず、4個の○で3×3のマス目に対して条件を満たすもの
1の場合は簡単。最初5行の上から順にどの列かを選ぶ5!と、最後に残った赤○配置可能な20個をかけ算。"5*4*3*2*20=2400"。
2の場合も一つ一つ積み重ねればなんとか。最初に青い2×2の枠を縦横5列から選ぶ "5C2×5C2"。青い枠内の配置は "2" 通り。赤い枠内は、縦横とも3列中1列を選び、交差したところ以外の4つに○を置くということで、"3×3" 通り。"10*10*2*3*3=1800"。
この2つを足し合わせれば答えです。プログラミングするまでもありません。
最後に
同じ数字を出すのに、切り口が違うと全然違うように見えるのが面白いです。
そして浜学園って懐かしいです。年齢が1/3くらいの頃に少しお世話になっていました。 …もうそんなに前の事(/-;


ご無沙汰しております。<br>ただでさえ数学が苦手だった上に長い事離れてるのでもはや何にも覚えてないのですが、ただ一つ「回転ありの順列組み合わせ」に苦しまされた事だけは記憶しているのでここでお聞きしたいのですが、これは回転すると重ね合わせられる図形については考慮されているのでしょうか。された場合とされていない場合の違いが見れたらなぁと思います…(それが理解できるかどうかはともかくとして←)
お久しぶりです。blogはしっかり読ませて頂いていますです。<br>回転については全く考慮に入れていません! たぶん条件を満たす物で180度回して重なるものは数えるほどしかない、と言うか下図+線対称な8通りしか思いつきませんでした。これで全てなら、だいたいは90度単位で回したものが4個あるからそれで割り、180度で重なるものは2個で割り算な、"(4200-8)/4 + 8/2" ではないかと。 <br><br>●□□□□ □●□□□ ●□□□□ □□●□□<br>□□●□□ □□●□□ □□●□□ ●□□□□<br>□●□●□ ●□□□● □●□●□ □●□●□<br>□□●□□ □□●□□ □□●□□ □□□□●<br>□□□□● □□□●□ □□□□● □□●□□<br><br>全く自信がありません。どなたかのツッコミを期待(汗)。
□□●□□<br>□●□□□<br>●□□□●<br>□□□●□<br>□□●□□ ミス。最初の1つはこちら…
mAFb3e <a href="http://xrdrexmeoldp.com/">xrdrexmeoldp</a>, [url=http://byploifrxvjh.com/]byploifrxvjh[/url], [link=http://rfsmebszxdku.com/]rfsmebszxdku[/link], http://urubyhrshdbj.com/