hossy online - といぼっくす
ゲームの感想日記、たまにIT・プログラミングの話
以前の日記
| 前 | 2010年 12月 |
次 | ||||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
- 04/01
- 12/19
- 04/26
- 1. Inscryption Kaycee's Mod いろいろ攻略
- 04/01
- 1. Inscryption 序盤いろいろ攻略
- 04/01
- 1. 英語配列キーボードにリベンジしてみた
- 04/01
- 1. 英語配列キーボードはそんなにプログラマー向きじゃなかった
- 09/06
- 1. 連鶴を折ってみた
- 07/24
- 1. パズドラ やっぱり乗算は悪い文明
- 05/29
- 04/10
カウンタ
- 合計:
- 今日:
- 昨日:
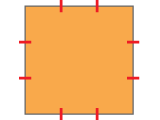
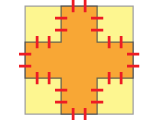


ちょっとエレガントかも?と感じたのを思いついたのでコメントさせて頂きます.<br><br>n 回目の状態での凸の数,凹の数をそれぞれ a_n, b_n とすると,凸の数は凹の数より必ず 4 つ多いので,<br>a_n - b_n = 4<br><br>n 回目の状態での橙色の部分の面積を c_n とする.n + 1 回目への変形操作において,凸部分にある正方形の面積が減少し,凹部分にある正方形の面積が増加する.その正方形の面積は {(1 / 3)^n}^2 = (1 / 9)^n なので,以下の漸化式が導かれる.<br>c_1 = 1<br>c_(n + 1) = c_n - (1 / 9)^n * a_n + (1 / 9)^n * b_n<br><br>変形すると,<br>c_(n + 1) = c_n - (1 / 9)^n * (b_n - a_n)<br>c_(n + 1) = c_n - (1 / 9)^n * 4<br><br>階差数列による一般化により,<br>c_n = 1 - Σ[k = 1, n - 1] (1 / 9)^n * 4 (n >= 2)<br><br>1 / 9 < 1 なので無限等比級数の計算より,<br>lim[n -> ∞] c_n = 1 - {4/9 / (1 - 1/9)} = 1 / 2<br><br>※a_n, b_n, c_n を一般化する必要は無い点がエレガントと感じた点ですw c_n は「一般化してない」と言っていいか怪しいかもですがw
投稿後ミス発見 orz<br><br>階差数列による… のくだりのΣにある (1 / 9)^n は (1 / 9)^k の間違いです orz
変形すると… の部分の b_n - a_n も a_n - b_n の間違いですね orz<br>どうしてこうなった ^q^