12/02
_ [パズル] 三分割を繰り返してみると 解答編

Twitterや日記コメントで解答ありがとうございますー。解答編です。頂いたコメントの方が丁寧でして、このエントリは微妙かもしれません(汗)。
1. 凹凸の数の変化から計算
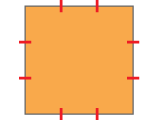
最初の面積が "1" なのと、次の面積は辺の長さ1/3の正方形4つ分減って "1 - 4*(1/3)*(1/3)" なのは良いと思います。
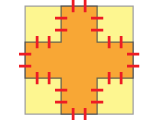
さて、凹凸の数は、いつも凸が凹より4個多くなります。最初の正方形が凸4, 凹0で、1回辺の長さを1/3に切っても凹凸の数が同じだけ増えるためです。ですので、毎回凸4個分の正方形の面積だけ、橙色の図形の面積が減ることになります。そして辺の長さは毎回 1/3 になります。すると、減る面積の1回目は "4*(1/3)*(1/3)"、2回目は "4*(1/9)*(1/9)"、3回目は "4*(1/27)*(1/27)" のようになっていきます。
これを順番に並べると:
| 回数 | 面積 |
|---|---|
| 0(最初) | 1 |
| 1 | 1 - 4 * 1/9 |
| 2 | 1 - 4 * (1/9 + 1/(9*9)) |
| 3 | 1 - 4 * (1/9 + 1/(9*9) + 1/(9*9*9)) |
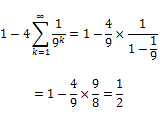
あとは左のような数列で解けます。面積1/2。
(このエントリのためにはじめて MS-Word2010の数式エディタを使ってみて、使いやすさにびっくりしました。リボンのコンテキストタブをうまく使って、自然に編集できる感じ。数式のお世話になっていた学生の頃にこれがあればと...)
2. 図を描くと


もう少し図を描き進めてみると、そのうち斜めを向いた正方形になりそうだと分かります。ぎざぎざ成分はどんどん小さくなっていくから、そのうち無視できます。ですから面積半分、終了。
斜めを向いた正方形に対してどれだけ凹凸があるか確認して、三角形4個分外側にはみ出している所から "k回目: 1/2 + 1/2 * 1/(9^k)" のような式を出すこともできます。けれど、そこまでしなくてもと。
最後に
無限に繰り返すというあまり直感的でないものが、図で描いてみると違って見えて面白かった、という事で取り上げたエントリでした。

