05/05
_ [プログラミング] 同じ問題を色々なプログラミング言語で解いてみる
はじめに
お知り合いさんの一部で、Project Euler (英語)、(日本語訳) という数学の問題をプログラムで解く企画が流行っています。290問あり、どれだけの数を解けるか競っているようです。どの問題も頑張れば1分以内に解けるように作られているそうなのですが、下手にプログラムを書いてしまうと1日経っても終わらないという。
多くの問題を解くのは色々な方が行われていますもので、逆に、簡単な1つの問題を多くの言語で解こうとしてみました。
問題: Problem 15
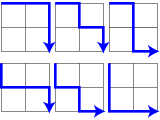
Problem 15 より:
左上の角から 2×2 のマス目を右下に後戻り無く進む方法は6通りある。では、20×20 のマス目では何通りか。
以下ネタバレです。
回答方針
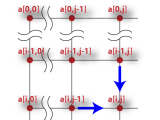
解く方針は主に2通りあると思います。
- ある枝分かれ箇所に着く方法は、上の枝分かれに着いて次に下に進むか、左の枝分かれに着いて次に右に進む場合。また、一番左と一番上は全て1通り。これで a[i,j] = a[i-1,j] + a[i,j-1] という表を更新する
- 左上から右下に向かうまでの(20*2)回の枝分かれで、右に進むのは20回。よって40個中20個の組み合わせ問題。40C20 = 40! / (20! * 20!)
どちらの方法でも桁あふれに注意です。正解は「137846528820」ですが、これが 2^37 強。32bit整数型では入れられません。64bit整数型か、52bit整数部を持っているdouble型 (IEEE754を期待) を使う事に。また、40! は 2^159 強で、それでも不足してしまいます。整数の桁数無制限を保証する仕組みが使えない場合には難しいです。
挑んだ言語一覧
TIOBE 2010/04 の言語人気ランキングを並べて書いてみます。
| 言語 | Position | 使用環境 | 1. | 2. |
|---|---|---|---|---|
| C | 1 | Pleiades 3.5 Galileo | ○ | |
| Java | 2 | Pleiades 3.5 Galileo | ○ | ○ |
| C++ | 3 | Visual Studio 2010 beta 2 (日本語) | ○ | |
| PHP | 4 | PHP 5.3.2 | ○ | ○ |
| (Visual) Basic | 5 | Visual Studio 2010 beta 2 (日本語) | ○ | |
| C# | 6 | Visual Studio 2010 beta 2 (日本語), RC (英語) | ○ | ○ |
| Python | 7 | Python 3.1.2 | ○ | ○ |
| Perl | 8 | ActivePerl 5.10.1.1007 | ○ | |
| JavaScript | 10 | Mozilla Firefox 3.6.3 | ○ | |
| Ruby | 12 | Ruby 1.9.1p378 | ○ | ○ |
| Go | 15 | go-windows (Nov 23, 2009) | ○ | |
| Lisp/Scheme | 23 | Gauche 0.9 | ○ | |
| D | 25 | DMD 2.045 alpha | ○ | |
| Haskell | 51-100 | Haskell 2010.1.0.0 | ○ | ○ |
言い訳。
- あまり効率は考えられていません
- それぞれの言語らしい書き方は多分できていません。普段使っているのが Ruby と C++ 位なものでして
- 片方の方針に挑んでいないのは、その言語でできないというわけではありません。多くは上のよう良く分かっていないだけです
- 整形はエディタお勧めに沿っています。ただしインデント幅は、表レイアウトの都合上、2に揃えています
文法の違いを見て楽しむくらいはできるのではと思います。たぶん。
回答一覧
| 言語 | 1. 2次元配列の数え上げ | 2. 40! / (20! * 20!) |
|---|---|---|
| C |
#include <stdio.h>
#include <stdlib.h>
int main(void) {
const int n = 20;
long long ary[n+1][n+1];
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
printf("%lld\n", ary[n][n]);
return EXIT_SUCCESS;
}
| |
| Java |
public class Euler015 {
public static void main(String[] args) {
final int n = 20;
long[][] ary = new long[n+1][n+1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
System.out.println(ary[n][n]);
}
}
| |
| C++ |
#include "stdafx.h"
#include <iostream>
int _tmain(int argc, _TCHAR* argv[])
{
const int n = 20;
long long ary[n+1][n+1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
std::cout << ary[n][n];
return 0;
}
| |
| PHP |
<?php
$n = 20;
$ary = array();
for ($i = 0; $i <= $n; $i++) {
$ary[$i] = array();
for ($j = 0; $j <= $n; $j++) {
if ($i == 0 || $j == 0) {
$ary[$i][$j] = 1;
} else {
$ary[$i][$j] = $ary[$i-1][$j] + $ary[$i][$j-1];
}
}
}
echo $ary[$n][$n];
?>
|
<?php
function factorial($n) {
$r = 1;
for ($i = 1; $i <= $n; $i++) {
$r = bcmul($r, $i);
}
return $r;
}
$n = 20;
$t = factorial($n);
echo bcdiv(factorial(2*$n), bcmul($t, $t));
?>
|
| (Visual) Basic |
Module Module1
Sub Main()
Const n As Integer = 20
Dim ary(n, n) As Long
For i = 0 To n
For j = 0 To n
If (i = 0 Or j = 0) Then
ary(i, j) = 1
Else
ary(i, j) = ary(i - 1, j) + ary(i, j - 1)
End If
Next
Next
Console.WriteLine(ary(n, n))
End Sub
End Module
| |
| C# |
namespace Euler015Cs
{
class Program
{
static void Main(string[] args)
{
const int n = 20;
long[,] ary = new long[n+1, n+1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
{
ary[i, j] = 1;
}
else
{
ary[i, j] = ary[i - 1, j] + ary[i, j - 1];
}
}
}
System.Console.WriteLine(ary[n, n]);
}
}
}
|
using System;
using System.Numerics;
namespace Euler015Cs2
{
class Program
{
static BigInteger factorial(int n)
{
BigInteger r = 1;
for (int i = 1; i <= n; i++)
{
r *= i;
}
return r;
}
static void Main(string[] args)
{
const int n = 20;
BigInteger t = factorial(n);
System.Console.WriteLine(factorial(2 * n) / (t * t));
}
}
}
|
| Python |
n=20
ary=[]
for i in range(n+1):
ary.append([])
for j in range(n+1):
if (i == 0 or j == 0):
ary[i].append(1)
else:
ary[i].append(ary[i-1][j] + ary[i][j-1])
print(ary[n][n])
| |
| Perl |
$n = 20;
@ary = ();
for ($i = 0; $i <= $n; $i++) {
for ($j = 0; $j <= $n; $j++) {
if ($i == 0 || $j == 0) {
$ary[$i][$j] = 1;
} else {
$ary[$i][$j] = $ary[$i-1][$j] + $ary[$i][$j-1];
}
}
}
print $ary[$n][$n];
| |
| JavaScript |
<script language="JavaScript">
<!--
var n = 20;
var ary = new Array(n+1);
for (var i = 0; i <= n; i++) {
ary[i] = new Array(n+1);
for (var j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i-1][j] + ary[i][j-1];
}
}
}
alert(ary[n][n]);
// -->
</script>
| |
| Ruby |
n=20
ary=[]
(n+1).times do |i|
ary.push []
(n+1).times do |j|
if (i.zero? || j.zero?)
ary[i].push 1
else
ary[i].push ary[i-1][j] + ary[i][j-1]
end
end
end
puts ary[n][n]
|
n=20
def factorial(n)
(1..n).inject(1){|r,i| r*i}
end
puts factorial(n*2)/factorial(n)**2
|
| Go |
package main
import ("fmt")
func main() {
n := 20;
var ary [21][21]int64; // n+1...
for i := 0; i <= n; i++ {
for j := 0; j <= n; j++ {
if (i == 0 || j == 0) {
ary[i][j] = 1
} else {
ary[i][j] = ary[i-1][j] + ary[i][j-1]
}
}
}
fmt.Print(ary[n][n])
}
| |
| Lisp/Scheme |
(define (fact_impl n r)
(if (= n 1)
r
(fact_impl (- n 1) (* r (- n 1)))))
(define (factorial n)
(fact_impl n n))
(define (func n)
(let ((t (factorial n)))
(/ (factorial(* n 2)) (* t t))))
(func 20)
| |
| D |
import std.stdio;
void main()
{
const int n = 20;
long[n+1][n+1] ary;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
writefln(ary[n][n]);
}
| |
| Haskell |
import Array
func :: Int -> Integer
func n = a!(n, n) where
a = array ((0, 0), (n, n)) (
[((0, j), 1) | j <- [0..n]] ++
[((i, 0), 1) | i <- [1..n]] ++
[((i, j), a!(i-1, j) + a!(i, j-1)) | i <- [1..n], j <- [1..n]])
func 20
| func :: Integer -> Integer func n = factorial(n*2) `div` (factorial(n) * factorial(n)) where factorial :: Integer -> Integer factorial 1 = 1 factorial n = n * factorial(n-1) func 20 |
あとがき
別エントリにします。
エントリにする直前にいくつかのコードを微修正したのですが、これで動かなくなっていたらどうしよう...
05/09
_ [プログラミング] 同じ問題を色々なプログラミング言語で解いてみた 弐
前回で一段落で、今回はあとがきのはずだったのですが、色々あってもう少し続けてみます。
Ruby / (40! / (20! * 20!))
階乗な方法、このように書き換えることができました。
- 40! / (20!*20!)
- (40!/20!) / 20!
- (40*39*38*37*36*35*34*33*32*31*30*29*28*27*26*25*24*23*22*21)/20!
- (40*39*38*37*36*35*34*33*32*31*30*29*28*27*26*25*24*23*22*21) / (20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1)
- 40/1*39/2*38/3*37/4*36/5*35/6*34/7*33/8*32/9*31/10*30/11*29/12*28/13*27/14*26/15*25/16*24/17*23/18*22/19*21/20
こうすると、どの時点でも整数ですし、途中の値が一番大きくなるのが最後 20 で割る直前ですから double 型で十分扱える精度。無限精度の整数なんて不要で、多分どの言語でも大丈夫でした。あああ。
これをコードに直すと、
p (1..20).inject(1){|r,x|r*(41-x)/x}
36文字。前のエントリは何だったのでしょう(-・;
C++ / (40! / (20! * 20!))
同じ方針で、2パターン + 比較対象にそのまま答えを書いたもの。
// A: 答えをそのまま書いた #include "stdafx.h" #includeint _tmain(int argc, _TCHAR* argv[]) { std::cout << 137846528820; return 0; }
// B: 計算。#include は省略
int _tmain(int argc, _TCHAR* argv[])
{
std::cout << 40LL/1*39/2*38/3*37/4*36/5*35/6*34/7*33/8*32/9*31/10
*30/11*29/12*28/13*27/14*26/15*25/16*24/17*23/18*22/19*21/20;
return 0;
}
// C: メタ関数。#include は省略
template <int N, int K>
struct Func
{
static const long long value = Func<N, K-1>::value * (2*N-K+1) / K;
};
template <int N>
struct Func<N, 0>
{
static const long long value = 1;
};
int _tmain(int argc, _TCHAR* argv[])
{
std::cout << Func<20, 20>::value;
return 0;
}
最後のは関数呼び出しをしているようにコード中からは見えるのですが、この関数の計算は実行時でなくてコンパイル時に行っているようで。3通り全て、Visual C++ 2010 の混合モードで見てみると、以下のように "0x20 * 2**32 + 0x184B1B34 = 137846528820" と、出力したい値がそのまま書かれていました。
std::cout << Func<20, 20>::value; 00A5139E mov esi,esp 00A513A0 push 20h 00A513A2 push 184B1B34h
...コンパイラ、頑張り過ぎではないでしょうか(-・;
Haskell / (40! / (20! * 20!))
pi8027さん から前のエントリにツッコミを頂きました。ありがとうございます。
func :: Integer -> Integer func n = factorial(n*2) `div` (factorial(n) * factorial(n)) where factorial :: Integer -> Integer factorial 1 = 1 factorial n = n * factorial(n-1) func 20
この where 以下の階乗計算は、"fractional n = product [1..n]" で置き換えられるそうです。ああ(汗)。というわけでこう短くなります。
func n = factorial(n*2) `div` (factorial(n) * factorial(n)) where factorial n = product [1..n]
ついでに、C++の最後の例の方法をそのまま書き換えたものも。
main = print $ func 20 20 where func n 0 = 1 func n k = func n (k-1) * (2*n-k+1) `div` k
Haskell / 数え上げ
同じくpi8027さんから頂いたコメントより。
main = print $ l!!20!!20 l = repeat 1:map (snd.mapAccumL (\a b -> (a+b,a+b)) 0) l
main = print $ iterate (scanl1 (+)) (repeat 1)!!20!!20
...ええと、最初にこれを見たときに、何が起こっているのかさっぱり分からずに、リファレンス検索ツール [href] を使って一つ一つ読んでいきました。ここでは下側の方だけを。以下、これがすらすら読める方には読み飛ばしてください。
まず、関数の区切り方を変えます。
main = print((iterate (scanl1 (+)) (repeat 1))!!20!!20)
!! は配列の要素を返すもので、他の言語では [] や () になる事が多いです。print はそのまま表示するで、結局、
(iterate (scanl1 (+)) (repeat 1)) で得られる二次元配列の [20, 20] 番目を表示する
という事を表しています。
次、(repeat 1)。これは、1 が無限の続く配列。[1, 1, 1, 1, ...]。無限と言っても、最後に [20, 20] 番目が欲しいとなると、その計算に必要な所まで無駄なく調べるそうです。
その次、(scanl1 (+) l)。2つめの引数で指定した配列に対して、1つめの引数で指定した演算方法でつなぎ合せ、その場所まで計算した配列を返します。 ...言葉より、下の表を見た方が早いかと。
| 回数 | 式 | 配列 |
|---|---|---|
| なし | (repeat 1) | [1, 1, 1, 1, 1, 1, ...] |
| 1回目 | scanl1 (+) $ (repeat 1) | [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1, 1+1+1+1+1+1, ...] = [1, 2, 3, 4, 5, 6, ...] |
| 2回目 | scanl1 (+) $ scanl1 (+) $ (repeat 1) | [1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5, 1+2+3+4+5+6, ...] = [1, 3, 6, 10, 15, 21, ...] |
| 3回目 | 略 | [1, 1+3, 1+3+6, 1+3+6+10, 1+3+6+10+15, 1+3+6+10+15+21, ...] = ... |
| 20回目 | 略 | [1, 1+20, ..., 137846528820, ...] |
そして、この (scanl1 (+)) を 0回, 1回, 2回... と無限に繰り返した結果の配列を返すのが iterate関数。こうして二次元配列ができ、137846528820 という値が [20,20] 番目を見ることで取り出せるのでした。
Rubyで有限な範囲で書くとこんな感じ。
n = 20
ary = [[1]*(n+1)]
n.times do |i|
ary.push (0..n).collect {|j|
(0..j).inject(0){|r,x| r + ary[i][x]}
}
end
puts ary[n][n]
これをワンライナー(一行プログラム)で書けてしまうとは。Haskell凄い。
pi8027さん、どうも色々とありがとうございました。
あとがき
もう1つか2つ後のエントリに。
一言先に。前のエントリが、他にもぼけぼけしている書き方が混じっていないか不安になってきました(汗)。
05/10
_ [同人ゲーム] 東方活劇綺談 〜 第弐幕

[GATLING CAT] の今年の博麗神社例大祭作品、東方活劇綺談 〜 第弐幕。犬走 椛が主人公の、RPG要素のあるアクションゲーム。
前作にははまって、2009/06/06の日記 で紹介。となると、今回も期待していました。
面
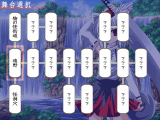

全14面+Ex3面のステージがあります。最初の3面は体験版でも楽しめます。
最初は「???」となっていて進めない所も多いです。クリアすると、少しずつ進める面が増えていきます。



雑魚戦。十字キーと、「通常攻撃」「スキル」「ジャンプ」「グレイズダッシュ」の4つのボタンを駆使して進んでいきます。前作にないスキルボタンで、かなり攻撃の幅が広がっています。コンボの締めなどに。
今回、前作以上にコンボが繋がりやすくなっています。マニュアルにもお勧めコンボが書かれている位に。良く分からなければ A・A・A だけでクリアでき... しましたが(汗)、多分いくつか身につけるとより良いかと。
コンボ中には得られる経験値やGOLDが増え、速く椛を成長させられます。頑張れば EXP*4 なども。スキル攻撃でもコンボが増え、たとえば巨大な敵の中でのの字弾幕を撃つと無敵+全弾ヒットで楽しいことになります。
各面で最大1回だけコンティニューできます。ただ、死亡回数が記録に残ってしまいます。気にする方は即リセット。
ボス戦


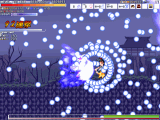
面の最後にボスが待ち構えている事があります。ちょっとした掛け合いの後に、ボス戦。今回の特徴は2つ。
一つ目、怒ゲージ。ダメージを与えるごとにゲージが溜まり、MAXになると必殺技を放ってきます。これにしっかり構えておかないと、下手すると即死もあります。でもコンボを繋いでいる時にはそこに集中して怒ゲージを見落とすのが、よくある事だったり。
二つ目、体力が残り1/4になった所で、硬くなったり攻撃が強化されたりします。この状態で怒MAXだったりするともう大変なことに。
特に後半のボスでは、グレイズダッシュで避けきれないような攻撃を多く行います。スキルを使って速攻で倒すなり、倒さなくてもスキル発動中の無敵時間を活用したりと、ボス戦ではスキルが要になります。
ま、とは言っても、ボスの攻撃パターンは単純で、見切ってしまえばなんとかなると思います。苦手な攻撃だけでもスキップすれば活路が開けるかと。多分。
RPG要素


成長の方法は3つ。
- レベルを上げる: 各種パラメータUP
- 武器精錬で強化する: 攻撃力UP
- 香霖堂で装備やスキルを買う: 防御力UP、スキル習得
経験値・GOLD・武器精錬に必要なアイテムは、全て各ステージで手に入れられます。効率よく稼げる所を探して何周もすれば、Ex3をクリアできる位には育てられるのではと思います。私はEx1ボスとEx3道中最後でコンボ数を稼ぎました。
スキルはどれが良いか迷うところです。そんなに高価なものでもないですし、色々試してみると良いのではと。
Ex3 は見廻りLv199、もみ主Lv155で突破。この時にはお金が余りました。そういえば前作でも最後には余ったような。
その他計算式
以下、間違っているかもしれません。まずは各Lvのパラメータ。
| 難易度 | 最大HP | 最大SP | 最大ATK | 必要経験値 | 評価倍率 |
|---|---|---|---|---|---|
| こいぬ | 96+(Lv-1)*約7 | 15+(Lv-1)*約3 | 1.48+(Lv-1)*0.12+(武器Lv-1)*0.32 | (Lv+1)^3 | 0.8 |
| 見廻り | 72+(Lv-1)*約7 | 12+(Lv-1)*約3 | 1.24+(Lv-1)*0.12+(武器Lv-1)*0.32 | (Lv+1)^3 | 1.6 |
| もみ主 | 64+(Lv-1)*約7 | 12+(Lv-1)*約3 | 1.00+(Lv-1)*0.18+(武器Lv-1)*0.32 | (Lv+1)^3 | 3.2 |
もみ主は、マニュアルに書かれている「ダメージが1.5倍、ボス戦前にHP・SPが回復しない、敵の弾幕が強化」や、他にも蓬莱の薬でのSP回復量が少なかったりと厳しいところが多いです。しかし、他の難易度に比べて火力1.5倍はとても大きいです。見廻り級より進行のテンポが良い感じ。Ex3の難易度は前作Ex2に比べると楽で、もみ主でも十分全クリアを狙えます。多分。
次に評価点。
| 項目 | スコア |
|---|---|
| 武器レベル | 32 * 武器レベル^2 |
| 獲得経験値 | 0.01 * 獲得経験値 |
| 最高連撃回数 | 5 * 最高連撃回数^2 |
| グレイズ回数 | 2 * グレイズ回数 |
| ボス撃破回数 | 256 * ボス撃破回数 |
| 被弾ペナルティ | -2 * 被弾回数 |
| 死亡回数ペナルティ | -256 * 死亡回数 |
スコアの鍵は最高連撃回数に思えます。しかしどこまで伸びるのやら。白狼牙・外式を中心にして805までは見ました。レベルが上がりすぎると火力も上がってコンボ数が伸びる前に敵を倒してしまうという問題もありますし...
コンボ数と経験値・GOLDのボーナスは... とりあえず繋げれば吉(適当)。
最後に
期待通りに楽しめました。アクションゲーム好き、椛好きにお勧めです。
05/19
_ [同人ゲーム] GDGD 第2回トークショー
GDGDが1年ぶりに帰ってきました。6/17 6/12(土) 12時〜17時に、[GDGD 第2回トークショー] が行われます。定員100名で、本日から予約受付中。ゲストと演目は以下の通り。
- HAta さん(サークル:小松菜屋)
- 侵略!小松菜メソッド実演。(短時間ゲーム製作のノウハウ公開)
- muracha さん(サークル:Easy Game Station)
- EGSの画面作りから見るゲームメイク
- tbn さん(サークル:大雪戦)
- 社会人サークルの同人ゲーム制作事情 〜これだからゲーム作りはやめられない〜
- Fifteen さん(サークル:disfact)
- 同人ゲームにおける二次創作
- naoki sagawa さん(サークル:こびとスタジオ)
- XboxLIVEインディーズゲームへの道(同人ゲーム編)
速攻で申込みしました。色々と楽しみです。
5/20 23:18追記: 思いっきり日付を間違えていました m(_ _)m


_ pi8027 [Haskell の右側のコードですが、 fractional n = product [1..n] でいいですよね。]
_ pi8027 [左側も、多分 Array を使う必要は無くて、 import Data.List main = print $ ..]