hossy online - といぼっくす

_ [技術] 三角形の面積とかけ算のこと

今月末に10万円くらいの [Oculus] 正式版と40万円くらいの [HoloLens] 開発版がリリースされて、10月には5万円くらいの [PlayStation VR] が出ると、今年はVR立ち上げが楽しみな一年です。最初はゲームの世界を中心に、そのうちリアルな世界でも使われるようになるのかなと。家電の操作説明がホログラムで浮かび上がる日も、とか。

そんな風に3Dが楽しみで、このあたりの仕組みについて調べている今日この頃。透視投影の行列式がなんとなく分かってきました。お世話になっている [Qiita] を使ってまとめて書いてみると面白いかもと思いつつ、先人が多々いる中で今更何の意味があるのかどうか(-・;

そこで一つ関連して、技術系の小ネタとして面積の問題を出してみます。

問題

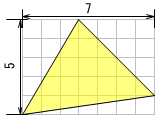
横7mm,縦5mmの長方形の中にある、黄色い三角形の面積を求めて下さい。

もしかしたら小学生から解ける問題のような、でも少し面倒なような。どのように求めるか、よろしければ少し考えてみて下さい。

例: 長方形から三角形3つを引き算

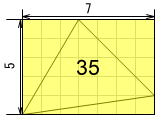
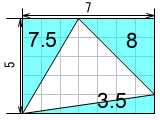
35-(7.5+8+3.5) = 16。素直な方法です。

例: 大きめの図形を求めてから引き算

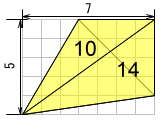
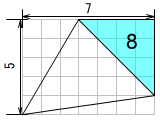
10+14-8 = 16。少し余計なところを求めてから引き算する、とすると計算を1回分減らせます。

例: 三角形を3つに分割

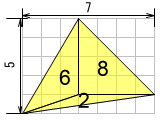
6+8+2 = 16。ここで切れば計算が少なく済みますが、方眼紙がないと気付きにくいと思います。

例: 三角形を変形

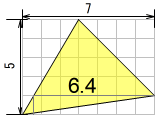
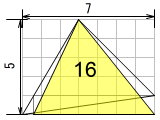
6.4×(4+1)÷2 = 6.4×5÷2 = 16。三角形の面積が底辺×高さ÷2で求まるなら、同じ底辺になる三角形2つにすれば、高さをまとめて三角形1つ分として計算できます。

6.4という長さを求めるのが少し面倒です。左上の線が縦:横=5:3だから、上に1進んだ時には横に0.6で、7-0.6=6.4、と。

例: ルート

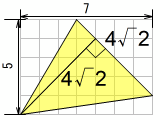
4√2×4√2÷2 = 4×4 = 16。直角二等辺三角形の辺の長さの比は 1:1:√2 から。右上の線に向かって垂線を落とすと簡単です。

しかしたまたま角度が45度だから良かっただけで、同じように他の2辺に垂線を落とそうとすると計算が大変になります。

他にも分割方法の違いとか、3辺の長さから面積を求める公式を使うとかもありますけれど、ここまでにして、

例: 外積

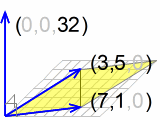
この問題をおそらく一番簡単に解く方法。(7*5-1*3)÷2 = 16 です。

平行四辺形の2辺を矢印で表した時に、両方の矢印に垂直で平行四辺形の面積を持つ、もう一本の矢印の計算方法です。XY平面上の平行四辺形だと、垂直なものは x, y とも0で、高さが (a_x*b_y-a_y*b_x) になります。

……これ確か小学生の頃に公式集で見て、滅多に使いそうにないのに式を1つ覚えるよりも三角形分割した方が安全じゃないと見なかったことにした覚えが。大学に入ってからやっと意味が分かりましたよ(汗。

ついでに内積

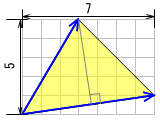
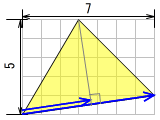
こちらは高校で習うものです。(a_x*b_x+a_y*b_y) = 7*3+1*5 = 26。これは傾いている2つの矢印の長さをかけ算するときに、どちらかの矢印の向きで行うというもの。斜め上に進んでいても矢印に接している方向にはこれだけ、というように垂線を落として、です。長さをかけ算して26なら、下辺の矢印の長さは √(7*7+1*1) = 5√2 で、右図の短い方の矢印の長さは 26÷5√2 と求まります。

内積は三角関数のcos, 外積はsinに対応、みたいな話もありますけれど、個人的には「投影した長さを求めるもの」か「法線と面積を求めるもの」か、という感じでとらえています。加法定理とか最近全然使っていません。

最後に

ATOK 2016と一緒に試している花子の練習を兼ねたエントリでした。

この手のグリッドに沿った作図、Microsoft Visio や Adobe FireWorks を使うとわりと描きやすいのですけれど、Visio は高いですし、FireWorksはCS6まででバージョンアップが止まりましたと。Illustrator, Inkscape, PaintShop Pro などはかっちりしたものが描きにくくてうーん。かといって2D CADを使うほどかっちりでもなく、うーん。

面積の問題としては、色々な解き方がありますというのと、外積が便利です、ということで。