05/05
_ [プログラミング] 同じ問題を色々なプログラミング言語で解いてみる
はじめに
お知り合いさんの一部で、Project Euler (英語)、(日本語訳) という数学の問題をプログラムで解く企画が流行っています。290問あり、どれだけの数を解けるか競っているようです。どの問題も頑張れば1分以内に解けるように作られているそうなのですが、下手にプログラムを書いてしまうと1日経っても終わらないという。
多くの問題を解くのは色々な方が行われていますもので、逆に、簡単な1つの問題を多くの言語で解こうとしてみました。
問題: Problem 15
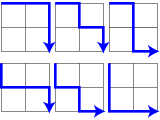
Problem 15 より:
左上の角から 2×2 のマス目を右下に後戻り無く進む方法は6通りある。では、20×20 のマス目では何通りか。
以下ネタバレです。
回答方針
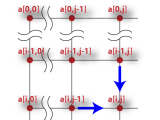
解く方針は主に2通りあると思います。
- ある枝分かれ箇所に着く方法は、上の枝分かれに着いて次に下に進むか、左の枝分かれに着いて次に右に進む場合。また、一番左と一番上は全て1通り。これで a[i,j] = a[i-1,j] + a[i,j-1] という表を更新する
- 左上から右下に向かうまでの(20*2)回の枝分かれで、右に進むのは20回。よって40個中20個の組み合わせ問題。40C20 = 40! / (20! * 20!)
どちらの方法でも桁あふれに注意です。正解は「137846528820」ですが、これが 2^37 強。32bit整数型では入れられません。64bit整数型か、52bit整数部を持っているdouble型 (IEEE754を期待) を使う事に。また、40! は 2^159 強で、それでも不足してしまいます。整数の桁数無制限を保証する仕組みが使えない場合には難しいです。
挑んだ言語一覧
TIOBE 2010/04 の言語人気ランキングを並べて書いてみます。
| 言語 | Position | 使用環境 | 1. | 2. |
|---|---|---|---|---|
| C | 1 | Pleiades 3.5 Galileo | ○ | |
| Java | 2 | Pleiades 3.5 Galileo | ○ | ○ |
| C++ | 3 | Visual Studio 2010 beta 2 (日本語) | ○ | |
| PHP | 4 | PHP 5.3.2 | ○ | ○ |
| (Visual) Basic | 5 | Visual Studio 2010 beta 2 (日本語) | ○ | |
| C# | 6 | Visual Studio 2010 beta 2 (日本語), RC (英語) | ○ | ○ |
| Python | 7 | Python 3.1.2 | ○ | ○ |
| Perl | 8 | ActivePerl 5.10.1.1007 | ○ | |
| JavaScript | 10 | Mozilla Firefox 3.6.3 | ○ | |
| Ruby | 12 | Ruby 1.9.1p378 | ○ | ○ |
| Go | 15 | go-windows (Nov 23, 2009) | ○ | |
| Lisp/Scheme | 23 | Gauche 0.9 | ○ | |
| D | 25 | DMD 2.045 alpha | ○ | |
| Haskell | 51-100 | Haskell 2010.1.0.0 | ○ | ○ |
言い訳。
- あまり効率は考えられていません
- それぞれの言語らしい書き方は多分できていません。普段使っているのが Ruby と C++ 位なものでして
- 片方の方針に挑んでいないのは、その言語でできないというわけではありません。多くは上のよう良く分かっていないだけです
- 整形はエディタお勧めに沿っています。ただしインデント幅は、表レイアウトの都合上、2に揃えています
文法の違いを見て楽しむくらいはできるのではと思います。たぶん。
回答一覧
| 言語 | 1. 2次元配列の数え上げ | 2. 40! / (20! * 20!) |
|---|---|---|
| C |
#include <stdio.h>
#include <stdlib.h>
int main(void) {
const int n = 20;
long long ary[n+1][n+1];
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
printf("%lld\n", ary[n][n]);
return EXIT_SUCCESS;
}
| |
| Java |
public class Euler015 {
public static void main(String[] args) {
final int n = 20;
long[][] ary = new long[n+1][n+1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
System.out.println(ary[n][n]);
}
}
| |
| C++ |
#include "stdafx.h"
#include <iostream>
int _tmain(int argc, _TCHAR* argv[])
{
const int n = 20;
long long ary[n+1][n+1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
std::cout << ary[n][n];
return 0;
}
| |
| PHP |
<?php
$n = 20;
$ary = array();
for ($i = 0; $i <= $n; $i++) {
$ary[$i] = array();
for ($j = 0; $j <= $n; $j++) {
if ($i == 0 || $j == 0) {
$ary[$i][$j] = 1;
} else {
$ary[$i][$j] = $ary[$i-1][$j] + $ary[$i][$j-1];
}
}
}
echo $ary[$n][$n];
?>
|
<?php
function factorial($n) {
$r = 1;
for ($i = 1; $i <= $n; $i++) {
$r = bcmul($r, $i);
}
return $r;
}
$n = 20;
$t = factorial($n);
echo bcdiv(factorial(2*$n), bcmul($t, $t));
?>
|
| (Visual) Basic |
Module Module1
Sub Main()
Const n As Integer = 20
Dim ary(n, n) As Long
For i = 0 To n
For j = 0 To n
If (i = 0 Or j = 0) Then
ary(i, j) = 1
Else
ary(i, j) = ary(i - 1, j) + ary(i, j - 1)
End If
Next
Next
Console.WriteLine(ary(n, n))
End Sub
End Module
| |
| C# |
namespace Euler015Cs
{
class Program
{
static void Main(string[] args)
{
const int n = 20;
long[,] ary = new long[n+1, n+1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
{
ary[i, j] = 1;
}
else
{
ary[i, j] = ary[i - 1, j] + ary[i, j - 1];
}
}
}
System.Console.WriteLine(ary[n, n]);
}
}
}
|
using System;
using System.Numerics;
namespace Euler015Cs2
{
class Program
{
static BigInteger factorial(int n)
{
BigInteger r = 1;
for (int i = 1; i <= n; i++)
{
r *= i;
}
return r;
}
static void Main(string[] args)
{
const int n = 20;
BigInteger t = factorial(n);
System.Console.WriteLine(factorial(2 * n) / (t * t));
}
}
}
|
| Python |
n=20
ary=[]
for i in range(n+1):
ary.append([])
for j in range(n+1):
if (i == 0 or j == 0):
ary[i].append(1)
else:
ary[i].append(ary[i-1][j] + ary[i][j-1])
print(ary[n][n])
| |
| Perl |
$n = 20;
@ary = ();
for ($i = 0; $i <= $n; $i++) {
for ($j = 0; $j <= $n; $j++) {
if ($i == 0 || $j == 0) {
$ary[$i][$j] = 1;
} else {
$ary[$i][$j] = $ary[$i-1][$j] + $ary[$i][$j-1];
}
}
}
print $ary[$n][$n];
| |
| JavaScript |
<script language="JavaScript">
<!--
var n = 20;
var ary = new Array(n+1);
for (var i = 0; i <= n; i++) {
ary[i] = new Array(n+1);
for (var j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i-1][j] + ary[i][j-1];
}
}
}
alert(ary[n][n]);
// -->
</script>
| |
| Ruby |
n=20
ary=[]
(n+1).times do |i|
ary.push []
(n+1).times do |j|
if (i.zero? || j.zero?)
ary[i].push 1
else
ary[i].push ary[i-1][j] + ary[i][j-1]
end
end
end
puts ary[n][n]
|
n=20
def factorial(n)
(1..n).inject(1){|r,i| r*i}
end
puts factorial(n*2)/factorial(n)**2
|
| Go |
package main
import ("fmt")
func main() {
n := 20;
var ary [21][21]int64; // n+1...
for i := 0; i <= n; i++ {
for j := 0; j <= n; j++ {
if (i == 0 || j == 0) {
ary[i][j] = 1
} else {
ary[i][j] = ary[i-1][j] + ary[i][j-1]
}
}
}
fmt.Print(ary[n][n])
}
| |
| Lisp/Scheme |
(define (fact_impl n r)
(if (= n 1)
r
(fact_impl (- n 1) (* r (- n 1)))))
(define (factorial n)
(fact_impl n n))
(define (func n)
(let ((t (factorial n)))
(/ (factorial(* n 2)) (* t t))))
(func 20)
| |
| D |
import std.stdio;
void main()
{
const int n = 20;
long[n+1][n+1] ary;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
ary[i][j] = 1;
} else {
ary[i][j] = ary[i - 1][j] + ary[i][j - 1];
}
}
}
writefln(ary[n][n]);
}
| |
| Haskell |
import Array
func :: Int -> Integer
func n = a!(n, n) where
a = array ((0, 0), (n, n)) (
[((0, j), 1) | j <- [0..n]] ++
[((i, 0), 1) | i <- [1..n]] ++
[((i, j), a!(i-1, j) + a!(i, j-1)) | i <- [1..n], j <- [1..n]])
func 20
| func :: Integer -> Integer func n = factorial(n*2) `div` (factorial(n) * factorial(n)) where factorial :: Integer -> Integer factorial 1 = 1 factorial n = n * factorial(n-1) func 20 |
あとがき
別エントリにします。
エントリにする直前にいくつかのコードを微修正したのですが、これで動かなくなっていたらどうしよう...


Haskell の右側のコードですが、<br>fractional n = product [1..n]<br>でいいですよね。
左側も、多分 Array を使う必要は無くて、<br><br>import Data.List<br><br>main = print $ l!!20!!20<br>l = repeat 1:map (snd.mapAccumL (\a b -> (a+b,a+b)) 0) l<br><br>これで解けますね。