04/01
_ [技術] 分かったつもりにならない3D計算 / はじめに
[Oculus]正式発売おめでとうございます。これを記念して、今日4/1から当サイトは3Dゲーム制作者を応援するサイトに変わります。(3Dゲーム作ったことありませんけれど)
そんなわけで、分かったつもりにならない3D計算講座をはじめてみます。これは「分かったつもりじゃなくて本当に分かる」という意味ではなく、きっと殆どの方がさっぱり分からないまま置いてきぼりにするという手抜きエントリです。 なにせこれを公開しようと思いついたのが2日前でして。ツッコミ所は多々あると思います。
_ [技術] 分かったつもりにならない3D計算 / 座標
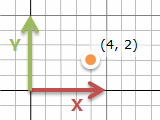
2次元の場合、点の場所を (x, y) の組で表します。右にいくつ、上にいくつとマス目を数えます。
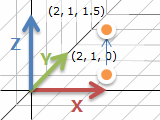
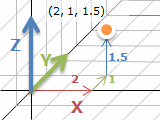
3次元の場合も、点の場所を (x, y, z) の組で表します。紙に描くのは大変ですけれど、行うことは同じです。
ここでは数学や OpenGL でよく使う右手系、右手親指から3つの指を直角に向けて、親指から順に x, y, z軸とします。画像は左上が (0, 0) ですとか、DirectX は左手系ですとかのツッコミは気にせず、このエントリではこの数え方で行きます。
座標軸の色。XYZの軸をRGBの色順で描くことが3Dソフトでは多いと思います。ほかでも赤緑青で並べることが多いと思います。たぶん。パズドラは赤青緑(火水木)とか違うものもありますけれど。
_ [技術] 分かったつもりにならない3D計算 / 平行移動・回転移動・拡大縮小
よく使う計算は「平行移動・回転移動・拡大縮小」の3つ。他にも鏡像や傾きなど、MS-Officeなどで見かけるような変形もできますが、それは別の所で。
平行移動
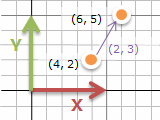
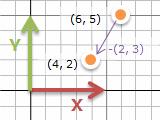
(4, 2) の場所から右に2, 上に3動くと (6, 5) になります。これを (4, 2) + (2, 3) = (4+2, 2+3) = (6, 5) のように書きます。
進んだ後に戻るのは引き算。(6, 5) - (2, 3) = (4, 2)。こういうのを逆算と言います。引き算は足し算の反対。普通は元に戻ります。(+∞とかしなければ)
3次元で z の数字が増えても、同じように足し算・引き算できます。
回転移動
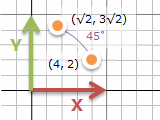
(4, 2) のものを原点 (0, 0) を中心に左回りに45°回転すると、(√2, 3√2) になります。逆算で右回りに45°回転すると (4, 2) に戻ります。
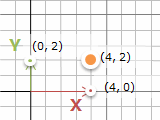
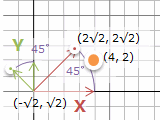
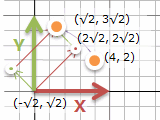
……√が出てきてなんだか難しいことをしている気分になりました。このときは、(4, 2) を横軸と縦軸の2つに分けて、それぞれ45°回転させたあとで足し合わせます。45°回転は 1 : 1 : √2 の直角に等辺三角形と同じ感じで、横軸が (2√2, 2√2), 縦軸が (-√2, √2) と分かれば、それぞれ足し算で終了。
一般的には、位置 (x, y) を角度 θ だけ左回りに回転移動すると、(x cosθ - y sinθ, x sinθ + y cosθ) になります。それぞれプラスとマイナスが逆で分かりにくいですが、θ=0°のときは全く移動しなくて (x, y) のまま、θ=90°のときには右上のものが左上に移る (-y, x) になる、と思うと、cos 0°=1, cos 90°=0 などから求められるでしょう。
3次元の場合は、この操作はZ軸に対しての回転になります。X軸回転の時は同じような式でy, zを変えてxはそのまま、Y軸回転のときはz, xを変えるようになります。では斜めの軸で回転させたいときは…… それはもっと先の方で。
縦横比固定の拡大縮小
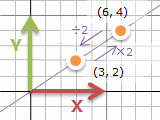
2倍の場所に動かすには、(x, y) をそれぞれ2倍します。逆算は、それぞれ半分にします。これは平行移動並みに簡単そうです。
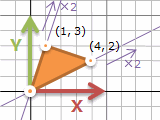
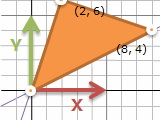
1つの点を動かすだけだと拡大に見えにくいですが、三角形の頂点をすべて動かすと、各辺2倍の拡大に見えます。
0倍すると元に戻らなくなります。3Dの計算は元に戻れることが大事。正射影・透視投影で平面上に3次元のものを映す時にも、Zを0倍とはしません。それはまた後ほど。
ここまでのまとめ
- 平行移動は足し算
- 回転移動はsin, cosの組み合わせ
- 拡大縮小はかけ算
_ [技術] 分かったつもりにならない3D計算 / 行列で回転・拡大
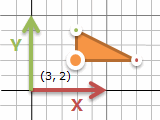
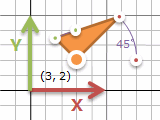
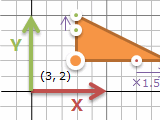
ここまでで平行移動・回転移動・拡大縮小ができました。そうすれば、三角形の左下を固定しての45°回転・1.5倍に拡大も組み合わせればできるはず。
と言いたいところなのですが、意外と面倒なのですよね……。なにせ回転・拡大ともに、計算式は原点 (0, 0) 中心でした。そのため、一度固定する場所を原点に平行移動して、回転や拡大して、また平行移動で元の場所に戻す、という感じに。例えば回転の方は、元の場所を (x, y) とすると、
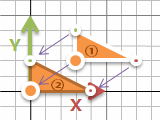
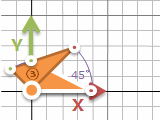
- ①: (x, y)
- ②: (x - 3, y - 2)
- ③: ((x - 3)・cos45° - (y - 2)・sin45° , (x - 3)・sin45° + (y - 2)・cos45°)
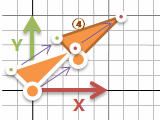
- ④: ((x - 3)・cos45° - (y - 2)・sin45° + 3 , (x - 3)・sin45° + (y - 2)・cos45°+ 2)
……回転1回でこんなに何度も計算をしたくありません。図を見れば下辺右の赤丸は (3, 2) から右上に4 = (2√2, 2√2) 進んだ場所で、 (3 + 2√2, 2 + 2√2) でしょうと。
どうしてこんなに計算が面倒かというと、平行移動・回転・拡縮が、それぞれ違う計算方法だったからです。右に1進んで更に右に2進むなら x + 1 + 2 = x + 3、2倍してもう一度2倍するなら x * 2 * 2 = x * 4 のように、同じ種類の計算なら一気に計算できます。なら、平行移動・回転・拡縮をすべて同じ方法に揃えれば良いじゃない。
それらをまとめられる考え方が、「行列」、2×2などの多数の数字の組です。回転と拡縮は次のような行列式になります。
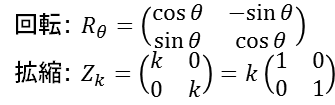
行列の計算方法は高校数学でたぶんあると思いますから省略。ぐぐってください。 (この日記に数式を書くのは面倒で……)
変な式に見えますが、(1, 0), (0, 1) が回転・拡大した時にどう動くかということを考えると、そのうちそらで書けると思います。
これを使って、45°回転と1.5倍を書いてみます。
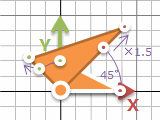
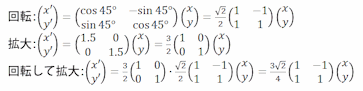
45°回転も1.5倍もかけ算。そうすれば、ある場所から45°回転して1.5倍するというのも、先に「45°回転して1.5倍するとどうなるか」を計算しておけば、1回のかけ算で終わります。簡単。
ところでこっそりと、座標 (x, y, z) の並びを縦に変えています。OpenGL 派でない方はこの座標の並びも行列の並びも計算順もひっくり返っていて読みにくいと思いますが、このエントリではこの並び順で進めます。
しかし困ったことに、どうかけ算しても平行移動を表す足し算にはなりません。工夫が必要になります。
ここまでのまとめ
- 回転移動と拡大縮小は、行列を使えばどちらもかけ算で行える
- 回転移動と拡大縮小の組み合わせは、行列のかけ算をして1つの行列にまとめられる
- 平行移動は難しい
_ [技術] 分かったつもりにならない3D計算 / 行列で平行移動も

この (-3, -2) 平行移動する方法です。 (だんだん〆切が迫ってきてペースアップ)
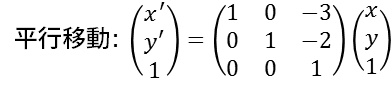
? (x, y) の2つしか欲しくないのに、なんだか行と列が1つずつ増えていますよ?
この式を展開してみると確かに、 "x' = x - 3, y' = y - 2, 1 = 1" と、平行移動になっています。最後の 1 = 1 は全然意味が無さそうですけれど、間違ってはいません。
そんな風に、座標の最後にダミーの 1 を付けることで、平行移動も行列で扱えるようになります。この座標を「同次座標」と言います。
今まで行列が2×2で済んだのに、ダミーのために3×3と倍以上のサイズになり、確かにかけ算できるようになったとしてもその割にはデメリット大きくない? という感じもします。でも、かけ算だけで済むメリットはやっぱり大きいのと、行列の成分が増えたようでもどうせ 0 と 1 が多くて、言うほど計算量は増えません。便利ですから使われています。
例

では前の三角形の移動を。(3, 2) を固定して45°回転したときに、座標がどう動くかを確認しましょう。(-3, -2) 平行移動して、45°回転して、(3, 2) 平行移動するのでした。
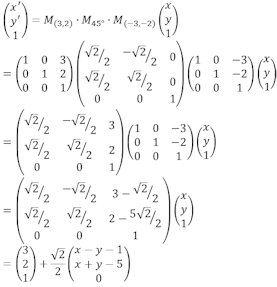
(3, 2) のときは右側がなくなって、元の座標が (1, 0) 増えると移動後は (√2/2, √2/2) 右上に長さ1だけ増え、元の座標が (0, 1) 増えると移動後は (√2/2, -√2/2) 左上に長さ1だけ増えます。あっていそうです。
こうすれば、平行移動・回転移動・拡大縮小をどれだけ繰り返しても、1回の行列計算にまとめられます。多関節などいくらでも難しいものをどうぞ。
3Dに拡張
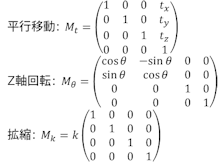
Zの行と列が増えますが、同じようなことをしているだけです。行列が大きくなっても 0 ばかりで、計算はそんなに大変ではありません。それに難しくてもどうせコンピューターが行いますし。
ここまでのまとめ
- 同次座標を使えば平行移動もかけ算で表せる
- 平行移動・回転移動・拡大縮小の組み合わせは怖くない
_ [技術] 分かったつもりにならない3D計算 / 座標系
座標系と逆操作

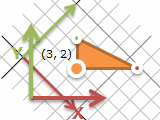
先ほどまでの移動は、点 (3, 2) を固定して三角形を45°右回転しても良いですが、三角形は固定して下の方眼紙を45°左回転しても、方眼紙の同じ場所に三角形の頂点があります。動かすものが変われば方向も変わります。
これを行うのが行列の割り算、逆行列です。ここでは省略しますけれど、うまく作れます。連立方程式を解ける、という使い方で見た方もいるでしょう。
45°回転を打ち消す-45°回転のように、(3, 2) 平行移動を打ち消す (-3, -2) の平行移動、1.5倍を打ち消す2/3倍の縮小、どれも行列の逆数でできます。
三角形の座標と方眼紙の座標は、お互いに行列と逆行列を使って行き来できます。と言うか、できるだけ行き来できなくなる変換はしないようにします。とりわけ怖いのが、0倍。例えば3次元のものを2次元のディスプレイ上に浮かべる時に、Zを0倍してなくしてしまえば良い、みたいに考えたくなりますけれど、そうすると2次元のディスプレイの座標からもとの3次元にどうやっても戻れなくなります。
カメラ
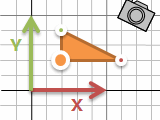
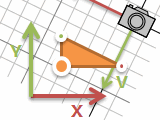
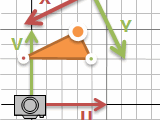
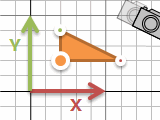
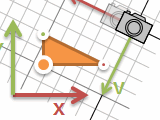
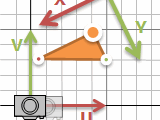
この座標の考え方をカメラではよく使います。カメラが動くと画面上でも動きます。三角形などそれぞれのモノをカメラにあわせて動かしていると大変。でもカメラの位置と座標系を変えるということなら、モノは動かさなくても大丈夫です。座標系を置き換える行列計算一回挟むだけ。
方眼紙の座標系で表した (x, y) がカメラの座標系でどんな (u, v) になるか、逆にカメラの座標系で表したものが方眼紙だとどうなるか、というように、お互いの世界を行き来できます。モノの座標系、方眼紙の座標系(ワールド座標系とかグローバル座標系とか)、カメラ座標系、いろいろな軸で考えられますが、どれもかけ算1回と考えると怖くありません。
_ [技術] 分かったつもりにならない3D計算 / 正射影と透視投影
さて、ここからカメラで写したものを、ディスプレイ上に映すにはどうなるか、というのを考えます。簡単のために、ディスプレイの大きさは (-1, -1) から (1, 1) までの正方形とします。ディスプレイの右をx, 上をyにします。ディスプレイの手前側が+z方向で、視線方向は反対側の -zです。
……と予定していた1/4くらい書いたところでもう4/1になって間に合わないので、ここからものすごくいい加減に。
正射影

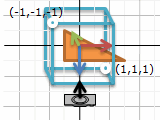
遠くの景色を見る時はほぼ平行と思って、正射影という方法が使えます。
画面に映したい場所が幅2の立方体に入れるように、平行移動・回転移動・拡大縮小します。描画する時には (x, y) をそのまま使い、z は奥のものが手前のものに隠れるように残しておきます。
これ、計算は簡単なのですが、3D表示としては近くのモノも遠くのモノも同じ長さだとさっぱり立体的に見えません。レースゲームで奥行きが感じられません。望遠鏡で覗くとかくらいの。製図とか長さが大事なとき向け、くらい。
メインは次の透視投影です。
透視投影
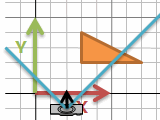
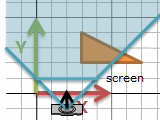
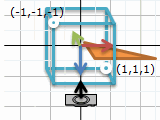
カメラからある角度の範囲内のものをスクリーンに投影します。四角錐を立方体にひしゃげるイメージ。
正射影のように立方体にしたいです。そのカメラから見た手前・奥の正方形に対応する、一番近い距離・遠い距離がどこか、という情報を使います。near plane とか far plane とかいうもの。すぐ目の前や無限遠は見えません。ま、目の前1mmのものを描いても困るから良いでしょう。
困ったこと。このようなひしゃげさせる変形は平行・回転・拡縮ではできません。いままでの行列計算はダメ。たぶん輪郭線だけなら、角座標のように考えれば行列なしでもなんとかなりそうです。でも、奥行き成分はどうなるの?
OpenGL の関数 glFrustum() に色が載っています。ええと、

……なんだか難しそう。
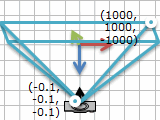
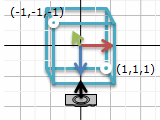
難しそうですので、具体例を考えてみます。スクリーンの位置はカメラから 10cm = 0.1m, 一番遠いところは1000mまで、スクリーンの縦横長さはスクリーンの位置の倍。
bottom = -left = 0.1, top = right = 0.1, near = 0.1, far = 1000. 画面の奥側は z マイナスですが、near, far はプラスの値にします。
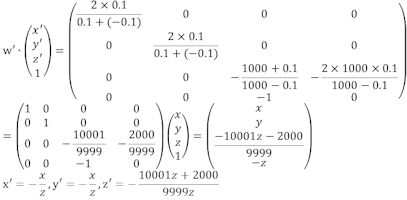
こっそりw'という成分が入っています。平行移動のときに出てきた同次成分のもう一つの使い方。
というように、x, yは割り算で x=±z, y=±z のときに立方体の外側になりそうです。zは良く分からないけれど z=-0.1 → z'=1.0, z=-1000→z'=-1.0 と、こちらも近い面と遠い面に対応していそうです。
おまけ: 一点透視法~三点透視法
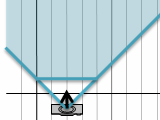
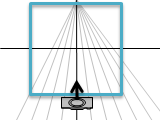
元の座標系でカメラからまっすぐ奥に1m間隔で平行線が延びていると考えてみます。幅1mだったとすると、手前の平面よりも広い幅ですが、一番奥の1000mに対しては誤差みたいなものでほとんど真ん中の一点に集まります。そうやって投影した座標系の方で一点に集めて描くと、美術で一点透視法した絵と同じようになります。
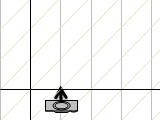
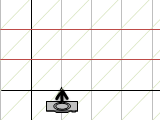
平行線ではなくて奥行きもつけてみましょう。別の角度で平行線を等間隔に描くと、交点の間隔が揃うはずです。今度はカメラの見る台形の右端と傾きが同じだから、投影後は立方体の右端に集まるはずです。
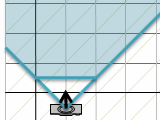
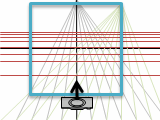
できました。
灰色のようにすべてのものが一カ所に揃うのが一点透視法になります。
また、緑線のように縦横交差した道路を斜めになるように見ると、もう一つの道路が別の点に集まった二点透視法になります。更にビルを見上げるようにもう一つの90°が別の場所に集まると三点透視法になります。美術と数学がちょっと繋がりました。
おまけ: zの精度
先ほどの例ですと、zは-0.1~-1000まで動けます。z'になったときに-1~1になることは分かりましたが、z'=0になるときのzはどこでしょう。
計算すると、z=-2000/10001≒-0.2 です。つまり10cm~20cmの範囲で、z'の立方体の領域の半分を使い切っている、ということ。z'の奥行きを使ってどちらが手前かを計算しようと思っても、けっこうぼろぼろな結果になります。うっかりすると奥のものが手前に見えてしまったり。
そうならないように、手前の平面と奥の平面の距離は必要最小限にしたいところです。
おまけ: 透視投影がリアルに見えないときは
透視投影はカメラから見た絵をディスプレイに映します。しかしそのディスプレイを見る人は、カメラと同じ位置にはいません。斜め方向から見ると歪んでいるような感じがして違和感が出ます。視野角が広くなればなるほどひどくなります。正面から見るとそこまでではないですが、奥行きが違って見えてやっぱり変な感じです。
3Dテレビとか3DSとかの3D表示が色々言われつつもふたを開けてみるといまいち流行らなかったのは、面倒さもありますが、このあたりの気持ち悪さにあるのかなと思いました。お勧めの位置に動いたり、3DSの奥行き設定を切り替えたりとか、なかなかできません。それらに比べると3D映画の受けが良いのは、ディスプレイの正面を向いていて、ディスプレイの大きさ・視野角から奥行きをチューニングできることがあるのかなと。
今年発売の OculusとかPlayStation VRとかHoloLensとかは、カメラの位置がいつも視点とぴったり合います。頭が揺れても、秒間60フレーム以上の速度で補正。Oculusを被っている人と、他の人が同じはずの画面を2次元のディスプレイで見ているのとでは全然感覚が違います。かぶる、というのはすごく面倒なのですけれど、リアルさが全然違います。ほんと流行って欲しいです。ゲームだけでなく、最近心臓手術のシミュレーションに使った、みたいなニュースがあって、凄いなと。
_ [技術] 分かったつもりにならない3D計算 / 行列以外の道具
はい、当然のように時間切れしました(-・; 3日前に思い立って書く量ではありませんでした。こんなのを2ページくらいでさらっと行列式だけ書いて終了している文献があるからたぶん少しくらい薄めて大丈夫かなと思っていたら、全然そんなことはなく。分かったつもりにもならない誰得エントリとなりました。
間に合えば図と共にかきたかったことを箇条書きにして終了とします。
複素数平面
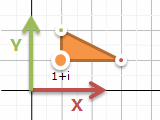
- √(-1)=iを、上下方向の軸で描いたもの
- x, y2つの実数を1つの数字で扱える
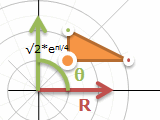
- eπi=-1 という式が好きな人が多い たぶん
- 平行移動は足し算、回転移動・拡縮はかけ算。2×2の行列と似ている
- XYの座標系と長さ角度の座標系を行き来して、それぞれ得意な計算するのが良い
- 便利だけれど、足し算とかけ算が分かれること、2値しか扱えなくて3Dには不向きなことから、CGとしてはたぶんあまり使わない
クオータニオン
- iみたいに実数に直交するものをj, kと増やして、4つの実数を1つの数字で扱えるもの
- i, j, k が対称なので扱いやすい
- しかしクォータニオンは4次元の概念で、3次元人には4次元立体のイメージがとても難しい
- 難しいから長さ1の超球面だけ考えるのがお勧め
- ヨー・ピッチ・ローを使って回転を考えようとすると、3つの値が全然対称でなくて計算が大変
クォータニオンだけでお腹いっぱいになるくらいの量になりそうな。来年の4/1にネタがなければと予告してみたり(汗。
それでは、エイプリルフールの残りも楽しみましょう、と。

